Numerical Analysis
In general, three methodologies stand out in the search for solutions to problems within the field of engineering, namely: analytical, experimental and numerical methods. To understand the numerical method it is necessary to know the others methodologies listed. In this article we will present the concept of the three methods and explore the use of numerical methods in solving engineering problems.
Numerical Analysis
The Analytical Method is used for less complex problems. It is a simple methodology that provides a direct answer when solving, usually manually, equations based on mathematical equations, in which input variables are defined to find the result of the output variables.
Analytical calculations cannot be applied to all challenges found in engineering, as the resolution of the equations which describe the studied phenomenon may be too complex to be calculated (for example: the resolution of second-order partial and nonlinear differential equations). To make the equations amenable to solution, the idealization of the physical characteristics that describe the phenomenon is adopted, making them much simpler than what is observed in practice. With this, the product obtained with the result of the equations by the analytical method can have considerable deviations in comparison to the real product, generating problems of oversizing, which increases the cost of production or implementation of a project.
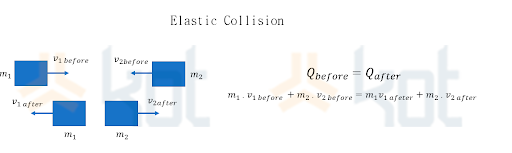
However, analytical solutions to simple problems can be used as a basis for understanding the behavior of the system of equations, for the development of numerical methods and for the verification of computational codes. To illustrate, the collision between two bodies can be classified as elastic when there is conservation of energy and the linear moment of the system, described by the equation shown in Figure 1. Therefore, most of the collisions found in nature cannot be classified as elastic, the consideration of this premise being a simplification to facilitate the application in specific cases.
Experimental Methods
Experimental methods use physical prototypes, which can be on a real or reduced scale, for the study of the phenomenon. Tests are carried out that simulate the operating condition of that product. Classic examples of the application of this methodology are the crash test of a car or the aerodynamic analysis of a Formula 1 car in a wind tunnel, as shown in Figure 2 [1].

Experimental methods present high quality in the results obtained and allow a detailed understanding of the studied event, however, a high investment is necessary. Such investment is not only characterized in relation to the cost of building the prototype, but also in relation to the investment necessary to obtain the essential infrastructure to accurately simulate the physical characteristics of operation. Another difficulty encountered when using the experimental method is in the time required to prepare the test, since it may be necessary to do several simulations and build different prototypes until obtaining an ideal design, mainly in destructive tests. Finally, some real conditions are not possible to be reproduced, for example, the simulation of oil reservoirs [2].
Numerical Method
The numerical method finds approximate numerical solutions to the most varied complex problems found in the real world, through applications of algorithms, which make it possible to elaborate and calculate mathematical operations using sequences of simpler arithmetic operations. “Numerical analysis idealizes and devises methods to efficiently approve the solutions of problems expressed mathematically” [3].
Algorithm is a finite set of ordered operations that makes it possible to solve a given problem. It consists of a series of specific instructions that, by means of a continuation of steps, make it possible to find an approximation of the result.
The numerical analysis aims to find an approximate solution of the real value through successions, using the least possible elementary operations. Despite having its beginning before computers, it is currently associated with information technology. As computers became more affordable and with greater processing capacity, the use of computational methods and techniques to solve real problems became popular, where manual resolutions can be impractical, imprecise, require a high financial investment or a long time for execution.
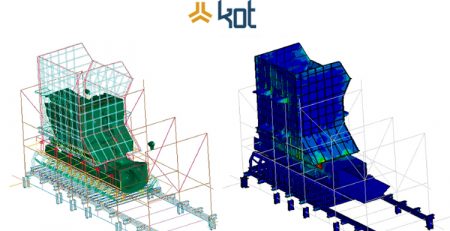
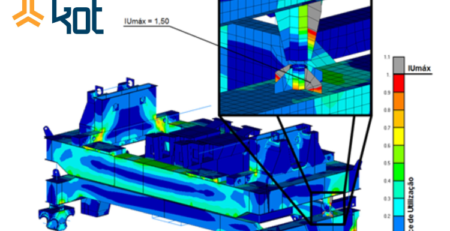
The numerical method is a methodology that requires an investment greater than the analytical method necessary, due to the need for a hardware infrastructure and software licenses, it still requires an investment lower than the experimental method. It is an approach that, regardless of the use of hypotheses that simplify the phenomenon in relation to that found in reality, still makes it possible to obtain a representation similar to that found in the study of a physical prototype in a shorter time. A practical application of numerical methods is the CFD simulation which, based on the laws of thermo fluid dynamics, seeks to solve the problem defined with the use of computational resources.
In the example shown in Figure 3, with the application of the CFD technique, it is possible to determine the pressure distribution over the entire external surface of a vehicle, determining aerodynamic drag and downforce coefficients, with a cost considerably lower than that of the test technique which takes place in a wind tunnel.

Numerical solution
In order to solve a problem using numerical solutions some requirements and stages should be considered, as can be seen on Figure 4 [3].
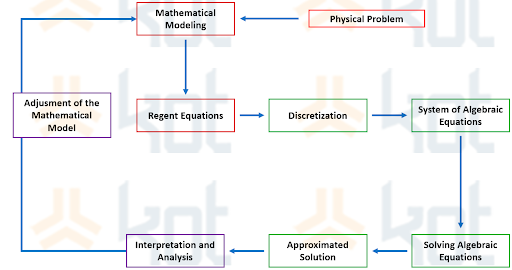
The mathematical model must be constructed from the observation of the phenomenon, using the laws of physics and mathematics. It needs to be constructed in such a way that it correctly represents the actual physical characteristics of the problem. With the mathematical model as reference, the numerical model is obtained, using the approximation method. This methodology is based on the discretization of the domain and the resolution of the differential equation at specifically pre-defined points.
The stages needed in the numerical solution can be summarized as:
Physical Model> Mathematical Model> Numerical Model> Numerical Solution> Numerical Results.
It is necessary to be careful in all stages of solving the analyzed problem to ensure that the numerical solution portrays the physical phenomenon reproduced. Otherwise, meaningless solutions can be obtained. “The numerical tool is appropriate and reliable when you have a numerical method that correctly solves the differential equations, and a mathematical model, which faithfully represents the physical phenomenon” [3].
The numerical solution can present two types of errors when the results found are compared with the physical problem in reality. Numerical errors are a consequence of incorrectly solving the differential equations. In this case, it is necessary to make a comparison of the result with other analytical or numerical solutions. There are also errors resulting from the use of equations that do not correctly describe the studied phenomenon.
Conclusion
The numerical method entails some advantages when compared to the other methodologies, amongst which are:
- Low cost when compared to the experimental method;
- Short time usage in the problem resolution;
- Ease of Simulating Realistic Conditions.
However, the numerical solution should not be seen as a substitute for other methods. It is the responsibility of the engineer in charge to analyze and determine what is the best methodology for solving the problem considering the advantages and limitations of each method.
Get in touch with KOT’s specialists team!

KOT Engenharia’s Team
With over 29 years of history and various services provided with excellence in the international market, the company promotes the integrity of its clients’ assets and collaborates in solutions to engineering challenges. For this integrity, it uses tools for calculation, inspection, instrumentation and monitoring of structures and equipment.
References:
[1] BARRETTO, Lawrence. First Look: Formula 1’s 2021 car in the wind tunnel. Formula 1, 21 de agosto de 2019. Disponível em: <https://www.formula1.com/en/latest/article.first-look-formula-1s-2021-car-in-the-wind-tunnel.6ye3S7Pb8NRX1K7PjTBxtS.html> Acesso em: 11 de abril de 2020.
[2] FRANCO, Admilson T. Métodos Numéricos Aplicados à Engenharia: Introdução aos métodos de diferença finitas e de volumes finitos. 2011. 9 f. Curso de Engenharia Mecânica, Departamento Acadêmico de Mecânica, Universidade Federal do Pará, Curitiba, 2011. Cap. 1.[3] ARAÚJO, Eduardo. Métodos Numéricos para Simulação na Engenharia. Blog ESS, 30 de novembro de 2017. Disponível em <https://www.esss.co/blog/simulacao-numerica-metodo-analitico-experimental-concorrentes-ou-complementares-na-engenharia/.> Acesso em: 20 de setembro de 2020.
[3] ARAÚJO, Eduardo. Métodos Numéricos para Simulação na Engenharia. Blog ESS, 30 de novembro de 2017. Disponível em <https://www.esss.co/blog/simulacao-numerica-metodo-analitico-experimental-concorrentes-ou-complementares-na-engenharia/.> Acesso em: 20 de setembro de 2020.








Leave a Reply