Para a solução dos desafios de Engenharia existem diversos métodos de simulações numéricas, cada um com suas particularidades e aplicações principais. O objetivo do presente artigo é apresentar as principais diferenças entre essas metodologias, como será descrito a seguir. A utilização do método dos elementos finitos (Finite Element Method – FEM) evoluiu com a melhoria na análise estrutural. Como exemplo, podemos citar a utilização de modelos reticulados (principalmente para a indústria aeronáutica) e evolução na utilização dos computadores, principalmente em meados dos anos 50 segundo alguns autores.
Já o método dos volumes finitos (Finite Volume Method – FVM) tem a preferência de profissionais que precisam lidar com mecânica de fluidos, podendo também ser utilizado na resolução de problemas que envolvam transferência de calor ou massa. O método dos elementos discretos (Discrete Element Method – DEM), por sua vez, é amplamente aplicado em fluxos granulares.
Conhecer a teoria por trás da modelagem matemática e computacional é essencial para entender melhor problemas de operação e como buscar soluções para problemas corriqueiros da engenharia. Neste artigo, conheça as diferenças entre os três métodos mencionados: FEM, FVM E DEM.
Método dos elementos finitos (FEM)
Inicialmente, o FEM foi utilizado em estudo de problemas da mecânica dos sólidos (para avaliação de tensões em asas de aviões). Em pouco tempo, se estendeu para aplicações envolvendo outros fenômenos físicos, tornando-o um método muito aplicado na indústria e na academia. Ele evoluiu passando de análises estáticas para dinâmicas; de problemas lineares a não lineares; de um único fenômeno a vários simultâneos que interagem entre si.
O método dos elementos finitos usa a discretização do sistema em vários elementos para resolver equações diferenciais, substituindo um número infinito de variáveis por um número limitado de elementos de comportamento conhecido. Os elementos são de dimensões finitas, originando o nome do método.
De acordo com o tipo e dimensão do problema, pode-se ter diferentes formas das divisões. Nestas, definimos os nós e malhas:
- Nós: os nós são os elementos finitos ligados entre si por pontos e podem se mover de acordo com a aplicação de carregamento, assim provendo respostas sobre o fenômeno estudado.
- Malha: a quantidade de nós irá representar o número de incógnitas que o problema terá e sua soma é conhecida como malha.
Essa metodologia resolve as equações matemáticas utilizando aproximações devido às subdivisões da geometria, logo a escolha da malha adequada é muito importante para a qualidade dos resultados. Sua precisão está relacionada à quantidade e tamanho dos nós e elementos, à qualidade da malha e ao tipo de função utilizada. Para uma melhor precisão, menor deve ser a área do elemento e maior a quantidade de nós e elementos na malha. Porém, um número muito grande de elementos acarreta no aumento do erro de arredondamento, podendo prejudicar a precisão do resultado e consumo de potência computacional.
Em suma, a geometria do que se quer analisar é dividida em elementos, que são pequenas partes que representam o domínio contínuo do problema. Dessa forma, é possível desenvolver a análise estrutural por meio de deslocamentos, deformações e tensões. Também é possível simular vários cenários e, assim, estimar o desempenho de um determinado produto em relação a resistência, rigidez e fadiga.
Em outras palavras, o método dos elementos finitos permite identificar se um produto ou componente analisado atende às normas requeridas, observar os pontos de concentração de tensão e entender o comportamento da estrutura diante de um carregamento. Portanto, o FEM permite aperfeiçoar a geometria do objeto antes mesmo da fabricação.
A tecnologia pode permitir a integração entre softwares usados para a criação da representação geométrica, denominados CAD (Computer Aided Design), e os softwares usados para a resolução do problema baseado no método de elementos finitos, denominados CAE (Computer Aided Engineering), deixando as análises mais rápidas e eficientes.
As etapas para a análise do método de elementos finitos estão listadas abaixo:
1. Construir o modelo CAD do sistema em análise;
2. Determinar as propriedades do material;
3. Construir a malha do modelo em software CAE;
4. Determinar as cargas e condições de restrição;
5. Buscar a solução;
6. Analisar os resultados.
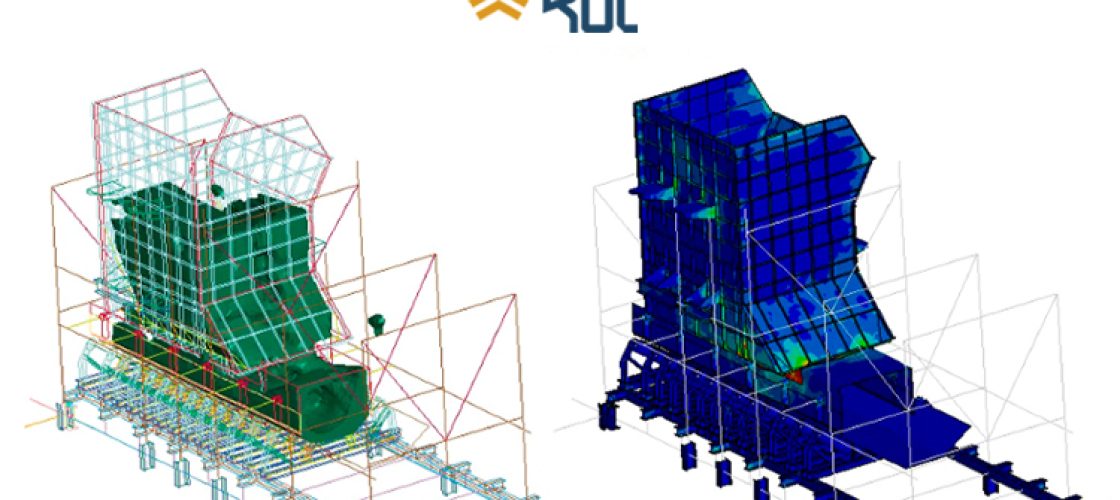
Um exemplo de aplicação de elementos finitos realizado pela Kot pode ser visualizado na Figura 1.

Figura 1: Aplicação prática de construção da malha com detalhes para os elementos finitos – FONTE: Acervo Kot.
Método dos volumes finitos (FVM)
Quando se trata do estudo de fluidos, deve-se obedecer às leis fundamentais da física no que se diz respeito à conservação de massa, quantidade de movimento e energia. Essas leis fundamentais nos levam às equações da continuidade, da energia e de Navier-Stokes. Essa trinca é comumente chamada de equações de Navier-Stokes, um conjunto de equações compostas por derivadas parciais que descrevem o comportamento dos fluidos.
O método numérico mais aplicável para resolver problemas de escoamento é o método dos volumes finitos. Neste, o domínio é decomposto em volumes de controle (VCs) para permitir o estudo de fluidos. Pode-se dividir o FVM , utilizado em softwares CFD (Computational Fluid Dynamics), em 3 passos:
- Pré-processamento do FVM
Inicialmente deve ser construída a geometria a ser trabalhada. Em seguida ocorre a subdivisão do domínio em partes menores, gerando uma malha de células, chamadas de volumes de controle (Figura 2). Também são identificadas as propriedades do material/fluido e incluídas as condições de contorno.
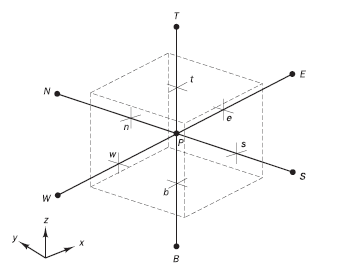
Figura 2: Representação de volume de controle – FONTE: Versteeg e Malalasekera, 1995.
- Simulação do FVM
Aqui, as equações de Navier-Stokes são aplicadas a cada um dos volumes de controle. Modelos físicos de turbulência, combustão, radiação, etc. são analisados por meio das equações numéricas. Conservação de massa, quantidade de movimento, energia e demais equações e variáveis de transporte determinam as condições da simulação. Todo o cálculo é realizado com base na aproximação das variáveis envolvidas e, uma vez que o sistema de equações estiver pronto, ele será resolvido conforme demanda cada caso, de forma segregada ou acoplada.
- Pós-processamento do FVM
Os resultados das análises são apresentados em gráficos e tabelas. Na utilização das ferramentas, também podem ser obtidas a distribuição de vetores na geometria e o perfil de distribuição de contorno. Assim, o que antes foi subdividido em volumes de controle, agora é analisado de forma global.
Apesar do método dos volumes finitos possuir características semelhantes ao FEM, o FVM é o mais indicado e usual para simulações da fluidodinâmica. Isso acontece porque as leis da termofluidodinâmica são melhor aplicadas em volumes de controle, principalmente em problemas relacionados a fluxos multifásicos, reativos, turbulentos ou de maior grau de complexidade.
Método dos elementos discretos (MED/DEM)
O método dos elementos discretos (MED) é utilizado quando se deseja calcular o escoamento, movimento ou dinâmica de um grande número de partículas discretas. Ele abrange tanto métodos computacionais que permitem a análise dos deslocamentos e rotações dos corpos discretos, quanto métodos que reconhecem automaticamente novos contatos à medida que os cálculos e iterações são executadas.
As análises iniciam a partir da descrição do movimento individual das partículas em cada incremento de tempo. O deslocamento das partículas é dado pela equação geral do movimento de Newton e pela equação de Euler para as rotações. Conhecendo o movimento, são estabelecidas as condições de contorno e/ou de operação e é possível chegar ao resultado desejado.
O DEM é notavelmente aplicado na simulação numérica de fluxos de materiais granulares com ou sem cominuição. Entre as principais aplicações, é possível citar:
- Modelos multifísicos que incluem escoamentos granulares;
- Formas complexas de partículas, em duas ou três dimensões;
- Movimentos complexos e com partículas de diferentes tamanhos interagindo entre si;
- Modelos de quebras de partículas (como britadores de minério);
- Prever probabilidade de quebra de partículas a partir do espectro de energia;
- Simulação do desgaste de superfícies.
Na Figura 3, pode ser visualizada a representação das partículas discretas em um software que utiliza o DEM.
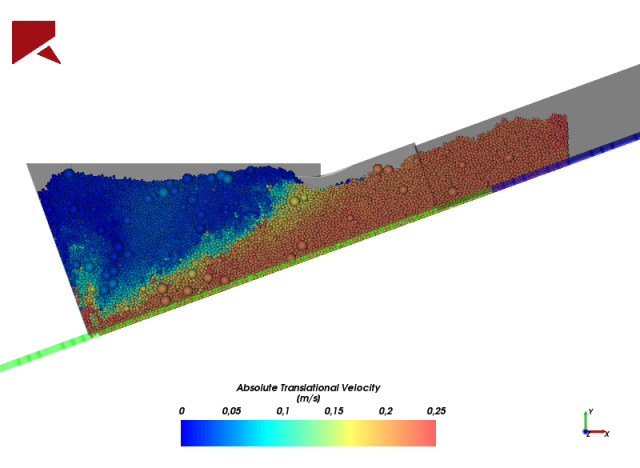
Figura 3: Representação de partículas discretas em modelo – FONTE: Acervo Kot.
Quando aplicar o FEM, FVM e DEM?
De forma geral, o FEM é utilizado em análises estruturais, o FVM abrange simulações de escoamentos e comportamento de fluidos e o DEM é aplicado para o movimento de partículas discretas.
Um exemplo prático seria o estudo de um silo em que ocorre o escoamento de cascas de frutas. Nesse caso, o material armazenado e escoado apresenta grande variação de seus parâmetros físicos, os quais são afetados, entre outras coisas, por: variações no período de colheita, variedade de fruta, processos anteriores e tempo decorrido em transporte. É possível conhecer o comportamento de cada material no silo e sua interferência na estrutura metálica.
Quando as cascas das frutas estão secas, seu escoamento deve ser determinado pelo método dos elementos discretos. Assim, é possível identificar regiões de entupimento, acúmulo de material, fluxo assimétrico, entre outras interferências comuns nesse tipo de operação. Esse exemplo pode ser visualizado na Figura 4.
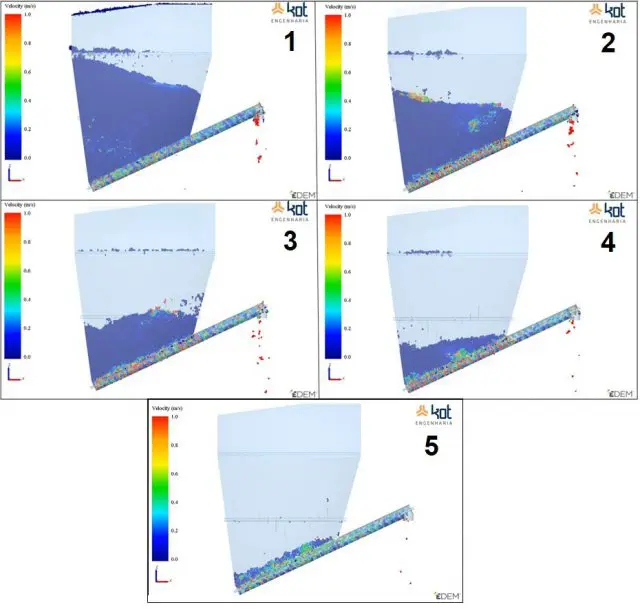
Figura 4: Escoamento de cascas secas em silo – FONTE: Acervo Kot.
Já na condição do material em que há alta umidade e a casca se apresenta como um material viscoso, seu escoamento é determinado pelo método dos volumes finitos. Nessa situação, é possível observar, por exemplo, como a viscosidade do fluido interfere no fluxo e quais são os impactos gerados. Veja um exemplo na Figura 5.
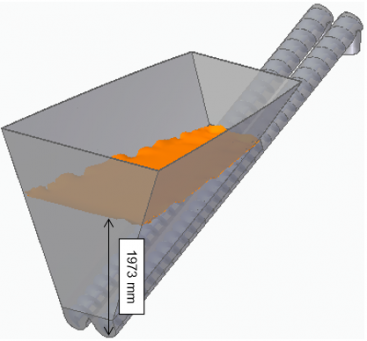
Figura 5: Altura do nível de fluido viscoso remanescente em silo – FONTE: Acervo Kot.
A partir das análises DEM e FVM/CFD, também é possível obter as cargas que o material, nas condições de operação, impõe na estrutura do silo. Assim, uma análise FEM deve ser feita tendo essas cargas como condições de contorno, conforme Figura 6.
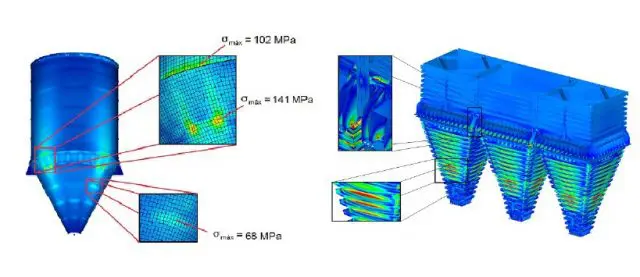
Figura 6: Análise pelo método dos elementos finitos de silo – FONTE: Acervo Kot.
Também é possível realizar análises que permitem visualizar, simultaneamente, os resultados de 2 ou mais métodos. É o caso de uma análise de avalanche realizada pela Kot, mostrada no vídeo. Nela, pode-se ver o escoamento calculado pelo método dos volumes finitos, enquanto a análise estrutural devido à avalanche é calculada pelo método dos elementos finitos.
Diversas são as formas de aplicar os métodos numéricos. É essencial compreender a teoria por trás de cada um para realização dos estudos computacionais que podem agregar valor de fato, solucionando problemas do dia a dia que desafiam a indústria. Para conhecer mais, consulte nossa equipe e saiba como a Kot Engenharia pode te ajudar a impulsionar os seus resultados.
Siga, também, nossas páginas no LinkedIn, Facebook e Instagram para continuar acompanhando nossos conteúdos.
Referência:
Malalasekera, W., and H. K. Versteeg. “An introduction to computational fluid dynamics.” The finite volume method, Harlow: Prentice Hall (2007): 1995.