Reading Time: 5 minutes

The knowledge of the accelerations and vibrations acting on an asset is essential for planning of predictive, planned, preventive and, in extreme cases, corrective maintenance actions on equipment and structures. These actions can optimize the equipment’s structural integrity when carried out assertively.

The Finite Element Method can simulate the behavior of these machines and structures when submitted to these accelerations and vibrations. Even if a structure is approved from the static point of view, the dynamic behavior may cause eventual structural collapse as a function of the vibration frequency of the oscillating equipment. To obtain these frequencies it is possible to use equipment capable of measuring vibrational data, such as camera/sensors and accelerometers.

This article aims to present, in detail, the use of the accelerometers to perform dynamic and vibrations analysis in structures.

 What is an accelerometer?

 Essentially, an accelerometer is an electronic sensor that can be fixed on the surface of the object of study from which you want to collect the data of acceleration and vibration. With this it becomes possible to determine the position of the body in space as a function of time [1]. One of these sensors can be seen in Figure 1. 

The method consists in the instrumentation of the asset with accelerometers at strategic points, connected to a data acquisition system that is responsible for the electronic recording of the collected information. To identify the points to be installed the sensors, a preliminary study is conducted to map the points most susceptible to variation in the values of acceleration and vibration.

An acquisition system commonly used in this type of test can be seen in Figure 2. After collecting the data, a computational treatment is performed to refine the values found. These results can be used as input into the computational model for structural verification.

Spring-mass system

The basic principles of an accelerometer originate from the physical system of a mass attached to a spring, known as the spring-mass system. This is a harmonic oscillator that restores its initial position from the force stored in the spring when removed from its original state by an applied force. Figure 3 shows a schematic of this system.

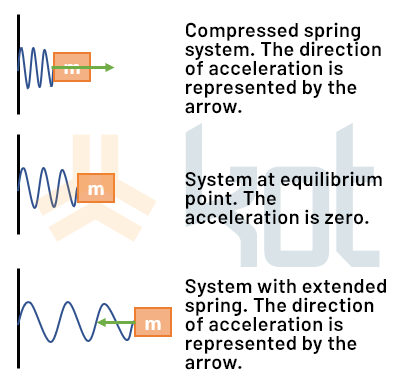
The equation for this movement is obtained from Newton’s second law of motion and is illustrated in Equation 1, where damping forces have been applied. These forces may come from air resistance, friction, or other dissipative effects.

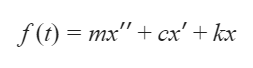
Where:

• f (t) = force as a function of time
• m = system mass
• x’’ = acceleration component;
• c = damping ratio (it varies mainly as a function of air resistance and friction)
• x’ = velocity component;
• k = spring stiffness;
• x = displacement of the mass relative to its equilibrium point. 

This model has great relevance in the study of natural phenomena, since it generates acceptable results for studies of small amplitudes of movement.

Like the spring-mass system, the mass present in the accelerometer causes deformations in the piezoelectric materials, internal to the sensor, which acts as strain gauges, generating an electrical charge proportional to the existing deformation. With the internal mass constant and the deformation generated, proportional to the electric charge, it is then possible to calculate the acceleration of the body. 

Accelerometers  Applications

The natural frequencies in theory depend only on the mass and stiffness of the system, which makes it possible to perform modal analyses with this information. These analyses consist of studies using the Finite Element Method to understand the structural responses to the natural vibration modes of the object. However, the available data are not always the real ones, and, in some cases, there is no information available. Thus, you can perform the instrumentation of an asset with accelerometers for calibration of the computational model.

Due to the characteristics of the equipment, it is common to use accelerometers on vibrating equipment such as sieves and crushers, as well as in buildings and structures that receive such equipment.

To establish the structural integrity of these assets it is essential to perform the applicable dynamic analyses. If the operating frequency of a machine is equal to its natural frequency, the phenomenon of resonance will occur, which amplifies the vibrations and can culminate in premature failure.

Figure 4 presents an example of vibration measurement at the base of a sieve, in a region near the spring, showing the locations where the accelerometers were fixed.

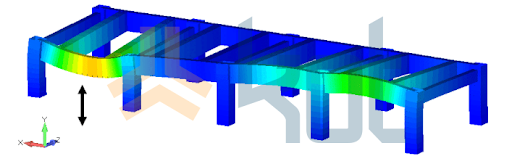
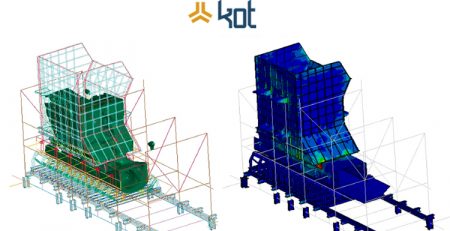
The results of the accelerometers measurements were used to feed the Finite Element Model of the base of the building in which the sieves are installed and Figure 5 presents the modal analysis of the structure for a specified natural frequency.

If you want to know more about Vibration Analysis and Dynamics of Structures check out Kot’s article on the subject by clicking here!

Conclusion

Although structures and equipment may not present problems in their static behavior, it is necessary to verify the natural frequencies of vibration to avoid the phenomenon of resonance that can lead to deterioration and premature failure of the system components. Kot has extensive experience in analysis of this nature and can evaluate different conditions and study scenarios in different oscillatory equipment. To learn more about the applications and what are the needs for the assets of your company, contact the team at Kot Engenharia!

Get in touch with KOT’s specialists team!

References:

[1] Jost. D. (2019/07/11). What is an accelerometer?. Available on: <https://www.fierceelectronics.com/sensors/what-accelerometer>

[2] Kot Engenharia’s archives.