Nonlinear analysis
Broadly speaking, mathematical analysis can be solved linearly and nonlinearly. In order to understand the situations in which nonlinear analysis is used it is important to know the circumstances for its execution. In this article we introduce the concepts behind both methods and explore the use of nonlinear analysis in the solution of engineering problems.
Stiffness
Initially, it is important to understand what is Stiffness and which are the main factors that can alter it. Such a concept can be presented as the load capacity to which a mechanical system can resist without drastically changing shape [1]. This means that it expresses the difficulty faced by the deformity under a certain tension.
The stiffness is directly linked to the following aspects:
- Material;
- Shape of the object;
- Kind of support bearing it.
It can be said that when a deformation on a structure does not surpass the elastic region of the material, the linear analysis is better suited as the material properties, shapes and support are not altered. On the other hand, when said deformation reaches the elasto-plastic region, it is crucial to use nonlinear analysis as at least one of these aspects suffers some sort of alteration.
Linear Analysis
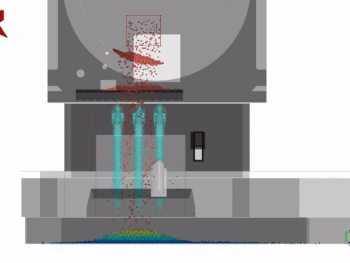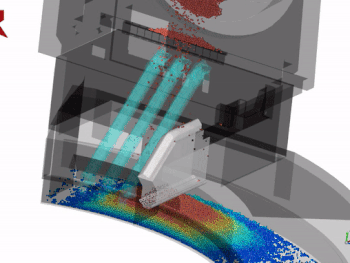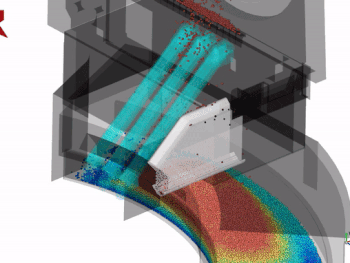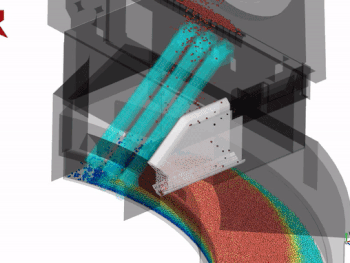
Linear analysis is used for less complex problems. It is a simplified methodology for the solution of real world problems. Thereunto, some mathematical and physics premises are adopted. Figure 1 represents the deformation of a cantilever.
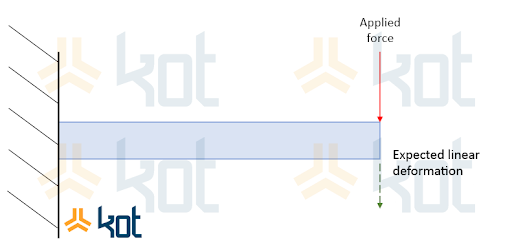
For the linear analysis of this situation, the beam illustrated is interpreted considering a small linear elastic deformation in the same direction as that of the green arrow, when under the load represented by the red arrow. This implies that, when a force is not applied, the structure will return to its initial state, without alterations. Thus, the physical analysis of the object can be accomplished in a simple manner with plausible results.
Nonlinear analysis
When the system in question does not present a linear behavior it is important to analyze it nonlinearly. The type of model presents a higher complexity. Figure 2 represents the nonlinear deformation of a cantilever.
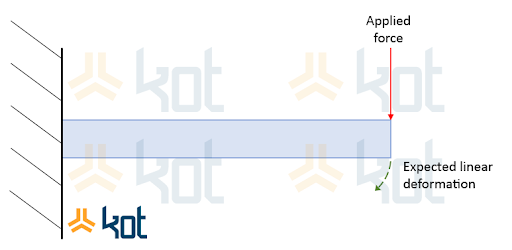
This kind of analysis enables the assessment of more diverse deformations where the system presents, among others, the following characteristics [3]:
- Nonlinear geometry;
- Nonlinear material;
- Buckling.
Linear v Nonlinear analysis
The table below expresses, in a summarised manner, the main characteristics of each of the types of analysis [4].
| Linear | Nonlinear |
| Are more simple; | Are more complex; |
| Are implemented faster; | Present more precise results; |
| Smaller intellectual and computational costs; | Higher intellectual and computational costs; |
| Present limitation to this kind of analysis. | Can be used in any context. |
Nonlinear Industrial Applications
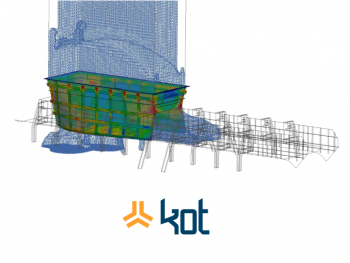
In order to clarify the application of the method, a case is presented below in which KOT performed a nonlinear analysis of a Roll Over Protective Structure, of the operating cabin of an off-road truck, according to the ISO 3471 standard [5].
The studied vehicle had the objective of transporting materials inside a mine. Later, it was proposed to adapt it so that it could act as a tugboat. In turn, it became crucial to remove the tipper from the truck, which made its cabin more exposed to possible overturns. Thus, KOT Engenharia carried out an analysis of the structure protection of the cabin considering the vehicle’s new functionality. Figure 3 presents the off-road truck without its bucket.

According to the material data provided by the manufacturer, it was clear the following stages of the study needed to follow a nonlinear approach, becausethe material presented a bi-linear behavior, as can be seen on Graphic 1.
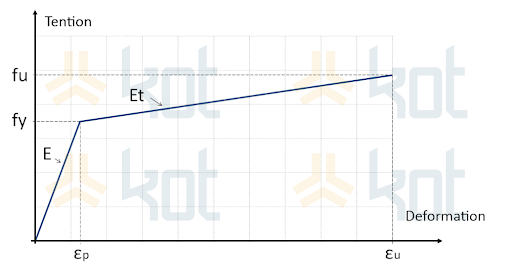
Where:
• fy is the yield stress limit;
• fu is the ultimate tensile strength;
• E is the modulus of elasticity;
• Et is the tangent plastic module, considering linear work hardening;
• εp is the maximum elastic deformation;
• εu is the ultimate tensile breaking deformation.
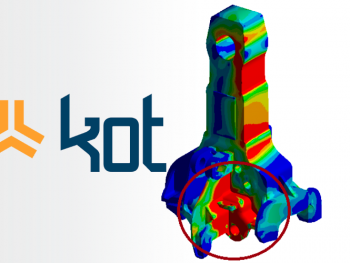
After the creation of the Finite Elements Method, the representation was exported to a LS-DYNA software, in which a nonlinear analysis was performed. Figure 4 presents the model created for the nonlinear analysis.
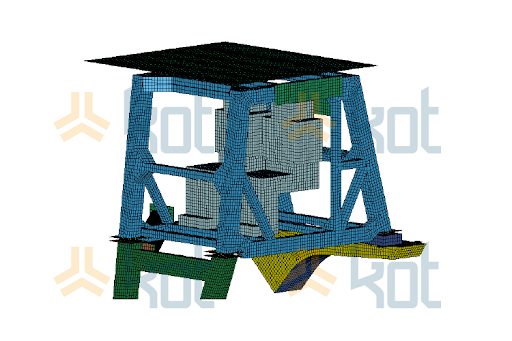
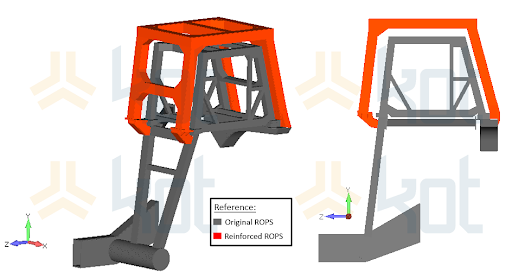
After the conclusion of the analysis, reinforcements to the truck protection structure were proposed as the original structure was not suited for the new conditions to be performed. Figure 5 illustrates the designed suggestions.
Conclusão
From reading this article you can easily conclude that nonlinear analysis is very useful in the context of engineering. KOT Engenharia has the necessary knowledge to apply it, also being able to assess different operational contexts, thus contributing to the precision of the results. Consult our team for more information.
Follow KOT’s blog and LinkedIn to ensure you are notified of our publications!
Get in touch with KOT’s specialists team!

KOT Engenharia’s Team
With over 29 years of history and various services provided with excellence in the international market, the company promotes the integrity of its clients’ assets and collaborates in solutions to engineering challenges. For this integrity, it uses tools for calculation, inspection, instrumentation and monitoring of structures and equipment.
References:
[1] Rogério Sales Gonçalves e João Carlos Mendes Carvalho. ESTUDO DA RIGIDEZ DE SISTEMAS MULTICORPOS.
[2] KOT Engenharia’s Archives
[5] ISO-3471:2008, Earth-moving machinery – Rollover Protective Structure – Laboratory tests and performance requirements.









Leave a Reply