Discrete Element Method: What is it?

Reading Time: 5 minutes

Background

In the last 40 years modern science showed a major advance in methodologies of computational analysis. This intense development of technologies, allied to new numeric methods, made possible to create theoretical models with daily applications to the companies.

The Continuum Mechanics theory was consolidated by Trusdell, Eringen and others scientists’ studies. Thereby, significant progress in comprehension of solid and fluids mechanics.

Even considering different types of nonlinearities, physical or geometrical, many engineering problems can be solved by using Numeric Methods. Nevertheless, the Continuum Mechanics Theory presents limitations. For instance, when a component is fractured, what in an anterior moment was supposed to be continuum, obviously stops being.

In front of this scenario, new methodologies related to experimental and empiric fields were created making it possible to achieve more confident analysis, despites the existing situations complexity, among them is the Discrete Element Method (DEM).

The rise of theoretical basis for method usually is associated with Cundall’s 1971 article, about a computational model simulating progressive, large-scale movement of block rocks. [1]. In 1979, Cundall was directly recognized for the DEM application in the article: “A discrete numerical model for granular assemblies” [2].

What is the Discrete Element Method?

The terminology DEM, covers both computational methods that allow analysis of dislocations, rotations, of discrete particles, including fracture, and also methods that automatically recognize new contacts as calculations and iterations are performed.

Thus, the DEM can be defined as a set of techniques suitable for simulating the dynamic behavior of multiple rigid or deformable bodies, which are subject to successives variations in contact conditions.

The Discrete Element Method is notably applied to the numerical simulation of granular material flow with or without comminution.

It is possible to differentiate the methods that use discrete elements, according to the particles categories, as in the case of rigid bodies, or by the modeling approach used, for example, the Discrete Lagrangian Theory.

The ordinary process of solving a problem using DEM begins with the description of the individual movement of the particles in each time increment. The displacement of the particles is given by Newton’s equations of motion and Euler’s equation for rotation.

Discrete Elements Methods application

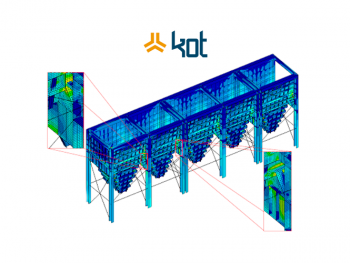
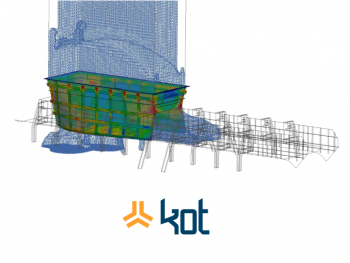
Softwares that use DEM can simulate, with precision, the behavior of granular materials from different formats and sizes, in different industrial machines such as industrial mills and transfer chutes.

To better illustrate, here follows an overview of DEM’s more common applications:

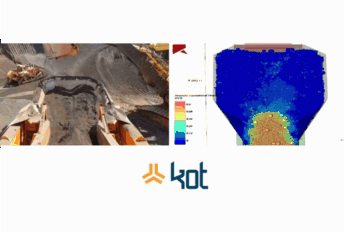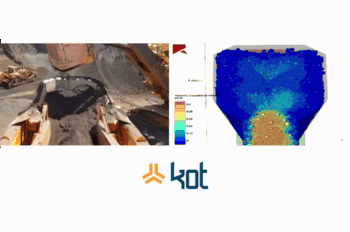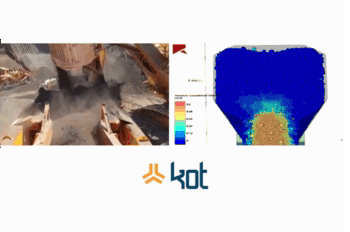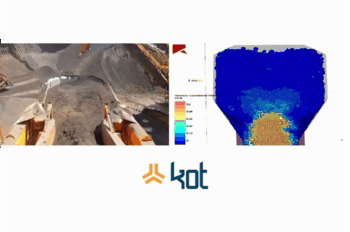
1 – Multiple physical models: DEM can be used associated and integrated with Computational Fluid Dynamics (CFD), Finite Element Methods (FEM) and Lattice-Boltzmann Method (LBM) to simulate multiphase and multicomponent fluids. Thus, scenarios such as the behavior of tractor structure (FEM) in a sandy environment (DEM) can be better studied. estrutura de um trator (MEF) em um meio arenoso (DEM) podem ser melhor estudados.

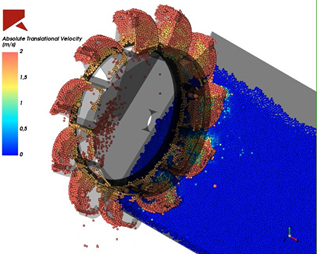
Figure 1 – DEM simulation predicting the loading of irregular particles and also FEM application at the blades of the structure
(Private archive from a KOT Engineering study case).

2 – Particles of complex format: particles can be designed in bi or tri dimensions for more appropriate reproduction of reality. This representation can be extended to rigids or flexible fibers modeling.

Figure 2 – DEM simulation for straw compression test, designed as fibers (credits: Rocky).

3- Complex Movements: movements with 6 degrees of freedom can be easily specified in DEM softwares so there are no restrictions or dependencies to Multibodies Dynamic softwares. In the next example, is presented a complex case simulation, where the particles have different sizes and simultaneously a mechanism alternates the flow in the chute.

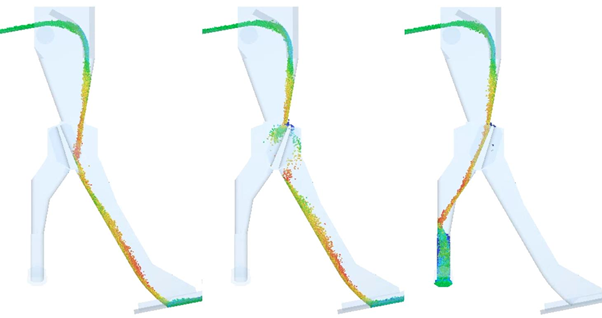
Figure 3 – DEM simulation for material flow in a chute, directed by a deflector (Private archive from a KOT Engineering study case).

4- Particle Breakage Models: related to well established models for simulating the particles breakage, such as: ABT10 and Tavares model. Some studies aim to avoid the breaking, others seek for the breakage.

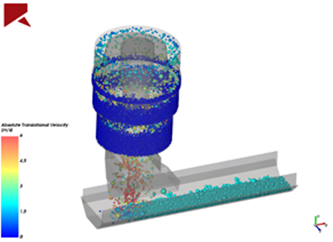
Figure 4 – DEM simulation of a secondary crusher used to break ore particles. (Private archive from a KOT Engineering study case).

5- Energy Spectrum: Through statistics models, DEM is used to predict the probability of particles breakage in a mixture of different materials (E.g: rocks and steel). The results are obtained over considerations of the materials’ properties and the energy spectrum of collisions.

Figure 5 – DEM simulation for different materials (Private archive from a KOT Engineering study case).

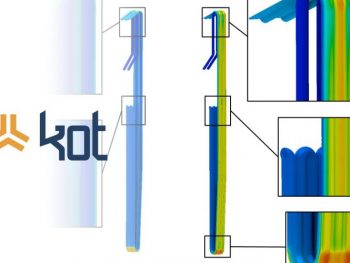
6- Abrasive Wear Model: It is possible to simulate the wear rate in equipment surfaces through the Archard wear equation by tribology studies.

Figure 6 – DEM simulation for Abrasive wear rate calculation of a crusher mill (credits: Rocky).

The Discrete Element Method opened the path for great advances in structural analysis of materials. However, in the same way that the Continuum Mechanics Theory had its own deadlocks, DEM presents limitations. What raises the question: Which are the next improvement steps that can be expected regarding the study of granular particles flow?

Companies can take advantage from the use and applications of Discrete Element Methods, in a whole universe of circumstances, as presented in this article. Softwares are the tools for using these methodologies, nevertheless the analysis process and study of cases still require professionals that not only master the theory basis, but also have vast practical experience. This way, those engineers will be able to extrapolate analytics results and create the best solution for each individual case.

KOT Engineering can be your partner in the application of DEM simulations, with the confidence, and practical experience in real complex cases that a referenced company requests.

KOT stands out in the national and international market offering high-level engineering services for large companies.

Get in touch with KOT’s specialists team!

Bruno de Freitas Brant

Mechanical / Aeronautical Engineer from UFMG and Master in Mechanical Engineering from the same university. He started his career in the area of 3D modeling, instructions for using software and technical support. Publications of articles focused on finite elements and rotor dynamics. In 2004, he took over as Technical Director at KOT Engenharia, where he leads multidisciplinary teams focused on solving engineering problems.

References:

[1]CUNDALL P. A. 1971. A Computer Model for Simulating Progressive, Large-scale Movement in Blocky Rock System . Available at: https://ci.nii.ac.jp/naid/10018723276/. (Accessed: 10/10/2020).

[2]CUNDALL P. A. Strack O. D. L. 1979. A discrete numerical model for granular assemblies. Available at: https://www.icevirtuallibrary.com/doi/abs/10.1680/geot.1979.29.1.47. (Accessed: 12/10/2020).

[3]Rocky. ESSS. What is Discrete Element Method and how does it work? Available at: rocky.esss.co/blog/what-is-discrete-element-method/. (Acessed: 1710/2020).