O que é o método dos elementos discretos (MED)?

Método dos Elementos Discretos: o que é?

Contextualização

A ciência moderna nos últimos 40 anos apresentou um grande avanço nas metodologias de análise computacional. O intenso desenvolvimento das tecnologias de computação, aliado aos novos métodos numéricos, tornou possível a criação de modelos teóricos com a aplicação no cotidiano das empresas.

A teoria da Mecânica dos Meios Contínuos foi consolidada pelos estudos de Trusdell, Eringen e outros pesquisadores. Com isso, houve avanços significativos na compreensão do comportamento de sólidos deformáveis, não deformáveis e fluidos.

Mesmo considerando diferentes tipos de não linearidade, tanto físicas como geométricas, muitos problemas de engenharia podem ser resolvidos por métodos numéricos. No entanto, a teoria da Mecânica dos Meios Contínuos apresenta limitações. Por exemplo, quando ocorre uma fratura em um determinado componente caracterizado por um material. O que em um momento anterior era suposto por contínuo deixa claramente de ser, comprometendo uma premissa da teoria.

Diante desse cenário, novas metodologias ligadas à área experimental e ao empirismo foram criadas possibilitando estudos mais confiáveis, apesar da complexidade do cenário real; entre elas o Método dos Elementos Discretos (DEM).

O surgimento da base teórica para o método normalmente é associado com um artigo de Cundall em 1971 sobre um modelo computacional em grande escala para o movimento progressivo de blocos de rocha [1]. Já em 1979, Cundall é reconhecido diretamente pelo aplicação de DEM pelo artigo “Modelo Numérico Discreto para montagens granulares”[2].

O que é o Método dos Elementos Discretos?

A terminologia Método dos Elementos Discretos (MED) ou Discrete Element Method (DEM) abrange tanto métodos computacionais que permitem a análise dos deslocamentos e rotações dos corpos discretos, incluindo a fratura, quanto métodos que reconhecem automaticamente novos contatos à medida que os cálculos e iterações são executadas.

Assim, o DEM pode ser definido como um conjunto de técnicas apropriadas para a simulação do comportamento dinâmico de um conjunto de múltiplos corpos rígidos ou deformáveis, que estão sujeitos às variações sucessivas das condições de contato.

O Método dos Elementos Discretos é notavelmente aplicado na simulação numérica de fluxos de materiais granulares com ou sem cominuição.

Pode-se diferenciar os métodos que utilizam elementos discretos, de acordo com a categorização das partículas, como no caso dos Corpos indeformáveis; ou pela aproximação da modelagem, por exemplo, a teoria de Discretos de Lagrange.

O processo comum de resolução de um problema pelo DEM se inicia pela descrição do movimento individual das partículas em cada incremento de tempo. O deslocamento das partículas é dado pela equação geral do movimento de Newton e pela equação de Euler para as rotações.

Aplicações do Método dos Elementos Discretos

O DEM é um método muito versátil por poder lidar e introduzir descontinuidades de uma maneira muito direta e intuitiva, ao contrário de outros métodos. Ademais, métodos discretos oferecem, por meio de modelos estatísticos, estratégias convenientes para a organização da desordem que a microestrutura dos materiais apresenta.

Softwares que utilizam DEM podem simular, com acurácia, o comportamento de materiais granulares de diversos formatos e tamanhos, em equipamentos como moinhos e chutes de transferência, dentre outros.

Para tornar o entendimento mais claro, segue uma visão geral dos tipos de aplicação mais comuns:

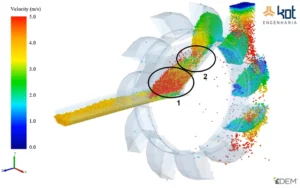
1 – Modelos multifísicos: o DEM pode ser utilizado em conjunto e de forma integrada com Dinâmica de Fluidos Computacional (CFD), Método dos Elementos Finitos (MEF) e Método Lattice-Boltzmann (MLB) para simular fluidos multifásicos e multicomponentes. Dessa forma, cenários como o do comportamento da estrutura de um trator (MEF) em um meio arenoso (DEM) podem ser melhor estudados.

Figura 1- Simulação DEM prevendo o carregamento de partículas irregulares e FEM aplicado na estrutura das pás.
(Acervo próprio de um estudo de caso, Kot Engenharia)

2 – Formas complexas de partículas: partículas podem ser desenhadas em duas ou três dimensões para uma melhor representação realística. Essa representação pode ser estendida para a modelagem de fibras que podem ser rígidas ou flexíveis.

Figura 2- Simulação DEM para um teste de compressão de palha, modeladas como fibras. (Créditos: Rocky)

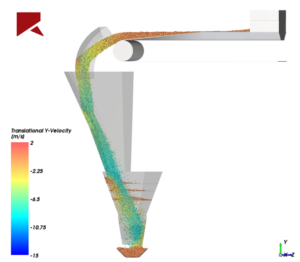
3 – Movimentos complexos: podem ser facilmente especificados. Movimentos livres com 6 graus de liberdade podem ser especificados em softwares de DEM para que não haja dependências com softwares de Dinâmica de Multicorpos. No exemplo abaixo, é simulado um caso complexo onde as partículas possuem tamanhos diferentes e simultaneamente um mecanismo alterna o fluxo no chute.

Figura 3- Simulação DEM para um fluxo de material em um chute direcionados por um defletor (Acervo próprio de um estudo de caso, Kot Engenharia).

4 – Modelo de quebra: modelos bem estabelecidos para simulação da quebra de partículas são utilizados, como: ABT10 e modelo Tavares. Para esses casos, alguns estudos procuram evitar a quebra das partículas e outros têm como objetivo a quebra.

Figura 4 – Simulação DEM de um britador secundário utilizado para quebrar partículas de minério. (Acervo próprio de um estudo de caso, Kot Engenharia).

5 – Espectro de energias: através de modelos estatísticos o DEM é utilizado para prever a probabilidade de quebra de partículas em uma mistura de diferentes materiais (Ex.: rocha e aço). Esse resultado é obtido através da consideração das propriedades dos materiais e espectro de energias de colisões.

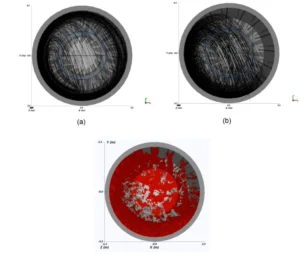
Figura 5- Simulação DEM para diferentes materiais em um moinho industrial. (Acervo próprio de um estudo de caso, Kot Engenharia).

6 – Modelo de desgaste: é possível simular o desgaste em superfícies de equipamentos de processamento através do Modelo Archard de desgaste na área de estudo pela tribologia.

Figura 6- Simulação DEM para simulação de desgaste em um moinho triturador (créditos: Rocky).

O Método dos Elementos Discretos permitiu grandes avanços nas análises estruturais de materiais. No entanto, da mesma forma que a Teoria dos Meios Contínuos apresentava impasses, o DEM também apresenta suas limitações. O que levanta a questão: quais são os próximos avanços que podem ser esperados no que se diz respeito ao estudo de fluxo granulares?

Empresas podem se valer do uso e da aplicação do Método dos Elementos Discretos nas mais diversas aplicações como demonstrado neste artigo. A execução de softwares é apenas a ferramenta para a aplicação destas metodologias. As análises e estudos de casos demandam profissionais que dominem não só a base teórica, mas que apresentem uma vasta experiência. Esses serão capazes de extrapolar resultados analíticos, gerando a melhor solução a cada problema proposto.

A Kot Engenharia pode ser sua parceira na aplicação desse método, com confiança, em cenários reais e complexos de engenharia.

A Kot se destaca no mercado nacional e internacional com oferecimento de serviços em engenharia de alto nível técnico para grandes empresas.

Entre em contato com o time de especialistas da Kot!

Bruno de Freitas Brant

Engenheiro Mecânico/Aeronáutico pela UFMG e Mestre em Engenharia Mecânica pela mesma universidade. Iniciou sua carreira na área de modelagem 3D, instruções de uso de software e suporte técnico. Publicou artigos voltados a elementos finitos e dinâmica de rotor. Em 2004, assumiu como Diretor Técnico na Kot Engenharia, onde lidera equipes multidisciplinares voltadas à solução de problemas de engenharia.

Referências:

[1] CUNDALL P. A. A Computer Model for Simulating Progressive, Large-scale Movement in Blocky Rock System. Disponível em: < https://ci.nii.ac.jp/naid/10018723276/>. Acesso em: 10 de Outubro de 2020.

[2] CUNDALL P. e Strack O. D. L. A discrete numerical model for granular assemblies. Disponível em: <https://www.icevirtuallibrary.com/doi/abs/10.1680/geot.1979.29.1.47>. Acesso em: 12 de Outubro de 2020.

[3] Rocky. ESSS. What is Discrete Element Method and how does it work? Disponível em: <rocky.esss.co/blog/what-is-discrete-element-method/>. Acesso em: 17 de Outubro de 2020.