Introdução

Primeiramente, falhas estruturais em equipamentos industriais nem sempre estão associadas à atuação de cargas excessivas ou a eventos extremos. Em muitos casos, estruturas metálicas rompem após longos períodos de operação sob tensões inferiores ao limite de escoamento do material, sem apresentar sinais visíveis de deterioração prévia. Esse tipo de falha está diretamente relacionado ao fenômeno da fadiga, sendo a mecânica da fratura aplicada à integridade estrutural uma abordagem fundamental para compreender e avaliar esses mecanismos.

A fadiga constitui um dos principais mecanismos de falha em estruturas submetidas a carregamentos cíclicos, como ocorre em equipamentos de mineração, sistemas de manuseio de granéis, portos e plantas industriais em geral. Em contraste com as falhas por sobrecarga estática, a fadiga se desenvolve de forma progressiva e silenciosa ao longo do tempo, podendo culminar em fraturas repentinas e de elevado impacto operacional, muitas vezes sem qualquer aviso perceptível. A Figura 1 ilustra o colapso de uma escavadora de roda de caçambas em decorrência de uma trinca por fadiga em um dos tirantes.

Figura 1 – Colapso de uma escavadora de roda de caçambas devido à falha por fadiga de um dos tirantes (Retirado de Rusiński et al. [1]).

Atualmente, dentre as metodologias disponíveis na literatura para a avaliação de vida em fadiga de um componente estrutural, destacam-se a fadiga controlada por tensão (método S-N), fadiga controlada por deformação (método ε-N) e a Mecânica da Fratura Linear Elástica (MFLE).

A priori, a Mecânica da Fratura parte do princípio de que é inevitável a presença de defeitos em uma estrutura, que podem estar atrelados ao processo de fabricação. Desse modo, mesmo que a estrutura nunca tenha entrado em operação, sua vida em fadiga pode estar comprometida, uma vez que a etapa de nucleação de uma eventual trinca já ocorreu, restando apenas a etapa de propagação.

Portanto, Mecânica da Fratura Linear Elástica tem se consolidado como uma ferramenta essencial para a avaliação da integridade estrutural, especialmente quando defeitos como trincas e regiões corroídas estão presentes nos componentes. Este artigo apresenta os conceitos fundamentais da Mecânica da Fratura, ilustrados por aplicações práticas reais em estruturas industriais analisadas pela Kot Engenharia.

Conceitos e definições

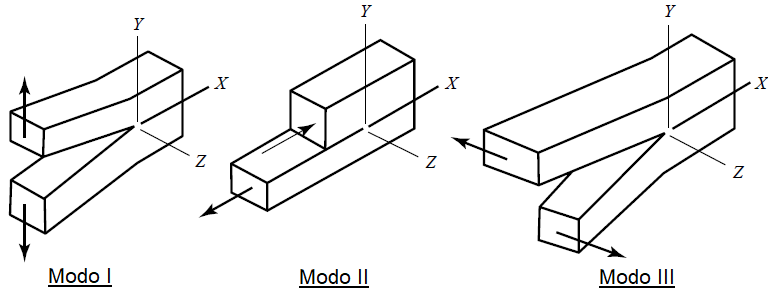
Existem três modos clássicos de propagação de trinca, caracterizados em função do deslocamento relativo entre as faces da trinca e do tipo de tensão associado. O Modo I corresponde à abertura da trinca por tração, o Modo II está relacionado ao deslizamento das faces por cisalhamento no plano da trinca, enquanto o Modo III refere-se ao rasgamento do componente devido à atuação de tensões cisalhantes fora do plano (torção, por exemplo). A Figura 2 ilustra esses modos de propagação.

Figura 2  – Modos de propagação de trinca.

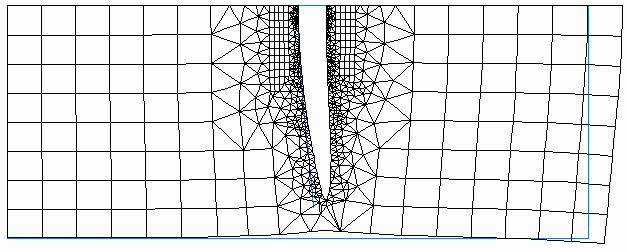
Nesse sentido, na Mecânica da Fratura Linear Elástica, o Fator de Intensidade de Tensões (K) é o parâmetro utilizado para se determinar a distribuição das tensões em torno da frente da trinca, permitindo avaliar o comportamento desta durante a etapa de propagação. O cálculo de tal parâmetro é realizado usualmente de maneira analítica, através das formulações disponíveis na literatura e em normas, como a BS 7910 [2] e a API-579 [3], mas também pode ser obtido por meio de ferramentas computacionais. Além disso, a vantagem deste último método é a possibilidade de análise de propagação de trinca em geometrias complexas, para as quais não estão disponíveis formulações teóricas que sejam perfeitamente compatíveis com a geometria em estudo. A Figura 3 mostra a modelagem computacional de uma trinca semielíptica em uma chapa.

Figura 3 – Modelagem computacional de uma trinca semielíptica (Retirado de Anderson [4]).

Em geral, o crescimento da trinca ocorre de forma estável durante grande parte da vida em fadiga (estágio II), conforme ilustrado no gráfico de estágios de propagação apresentado na Figura 4. Para o estágio II, a taxa de crescimento da trinca (da/dN) pode ser bem representada pelo ajuste de curva proposto pelo engenheiro e professor Paul C. Paris no início da década de 1960, dando origem à equação de Paris (Paris’s Law, em inglês). Por fim, na fase final (estágio III), ocorre o crescimento acelerado e instável da trinca, levando à falha catastrófica da estrutura. Neste momento, o fator de intensidade de tensões se iguala à tenacidade à fratura (K_IC) do material.

Figura 4 – Estágios de propagação de trinca (Adaptado de Lee et al. [5]).

Assim sendo, uma vez calculada a taxa de crescimento da trinca, torna-se possível determinar o tempo para que a trinca propague até atingir a instabilidade e, consequentemente, avaliar a vida em fadiga com base na Mecânica da Fratura. Para isso, é necessário realizar o processo de integração do inverso da taxa de crescimento da trinca partindo-se de um tamanho inicial de trinca até o tamanho final. Métodos de integração numérica, como a Regra de Simpson (veja aplicação na Figura 5), podem ser utilizados.

Figura 5 – Cálculo do tempo de propagação de trinca utilizando a Regra de Simpson (Retirado de Dowling [6]).

Mecânica da fratura como ferramenta de manutenção preditiva

A integração da Mecânica da Fratura Linear Elástica com estratégias de manutenção preditiva está alinhada à filosofia de projeto conhecida como fail safe. Nessa abordagem, admite-se a existência de defeitos, desde que a estrutura seja capaz de operar de forma segura até que o dano seja detectado e adequadamente reparado.

Dessa forma, ao estimar o tempo necessário para que uma trinca cresça até se comportar de maneira instável, torna-se possível definir intervalos de inspeção mais eficientes, priorizar intervenções em pontos críticos, reduzir paradas inesperadas e, consequentemente, aumentar a confiabilidade e a disponibilidade dos ativos industriais.

Essa metodologia permite, portanto, uma gestão da integridade estrutural baseada em dados técnicos e no comportamento real da estrutura, em substituição a critérios puramente empíricos.

Diversas técnicas de inspeção podem ser utilizadas para a detecção de trincas em estruturas, variando-se desde uma simples inspeção visual até a aplicação de técnicas mais avançadas como ultrassom e raios X. Entretanto, ao avaliar a integridade estrutural de um equipamento, deve-se ter em mente que a técnica de inspeção a ser adotada definirá o mínimo tamanho de trinca detectável (ad). Assumindo-se que uma estrutura possa conter uma trinca desta magnitude, poderá haver a propagação até que o comprimento crítico (a_c) desta seja atingido.

Ao se detectar uma trinca e realizar o seu reparo, é necessário que uma inspeção final seja executada para certificar que nenhuma trinca permaneceu na estrutura e, neste caso, admite-se que a integridade estrutural foi restaurada. Quanto maior o tamanho da trinca, maiores as chances de detectá-la. Entretanto, na realidade, sabe-se que não há garantias de que 100% das trincas tenham sido eliminadas, dado que existe um tamanho mínimo detectável associado ao método de inspeção empregado. Por essa razão, torna-se imprescindível a realização de inspeções periódicas para que a probabilidade de detecção seja maximizada e os riscos de falha da estrutura sejam minimizados. A relação entre o crescimento de uma trinca e a execução de inspeções periódicas pode ser melhor visualizada na Figura 6.

Figura 6 – Relação entre o crescimento de trinca e a execução de inspeções periódicas (Adaptado de Dowling [6]).

Aplicações práticas: exemplos de estruturas analisadas pela Kot Engenharia

Eixo de um britador

A Kot realizou a análise de uma falha que ocorreu no eixo de um britador. O equipamento em questão teve uma mudança no material manuseado e passou a britar um mineral com dureza mais elevada em relação à operação prévia. A Figura 7 mostra a ruptura do eixo em questão.

Figura 7 – Ruptura do eixo do britador.

Durante a análise da falha, desenvolveu-se um modelo em elementos finitos em software específico, conforme ilustrado na Figura 8. Além disso, foram realizadas as seguintes etapas:

• Investigação visual da estrutura do eixo após a quebra;
• Análise laboratorial das propriedades mecânicas do eixo;
• Análise estática através do método dos elementos finitos;
• Análise de fadiga multiaxial utilizando o método S-N;
• Avaliação da resistência do eixo considerando a seção fragilizada devido à presença de uma trinca.

Figura 8 – Modelo em elementos finitos do eixo do britador.

Em conclusão, após o término da investigação, foi possível concluir que a falha do eixo foi causada pela associação de dois fatores: sobrecarga decorrente da queda de um material não britável no equipamento e integridade do eixo fragilizada devido à existência de uma trinca em sua superfície, próximo ao rasgo da chaveta. A superfície de fratura do eixo pode ser vista na Figura 9.

Figura 9 – Superfície de fratura do eixo do britador.

Análise de mecânica da fratura em recuperadora

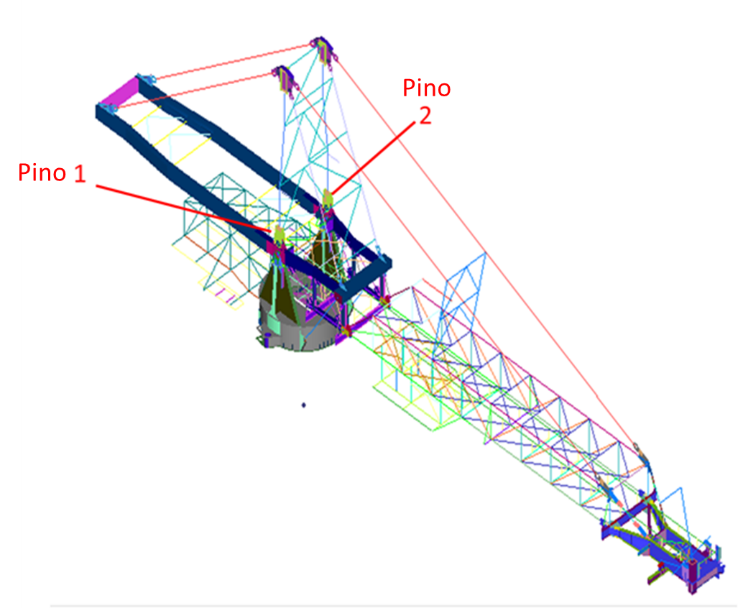
A Kot Engenharia realizou a análise de mecânica da fratura do pino inferior do mastro de uma recuperadora de roda de caçambas. A empresa cliente, por meio de inspeção por ultrassom, detectou trincas similares nos pinos do lado esquerdo e direito da máquina. A identificação dos pinos pode ser visualizada na Figura 10.

Figura 10 – Identificação dos pinos avaliados na recuperadora.

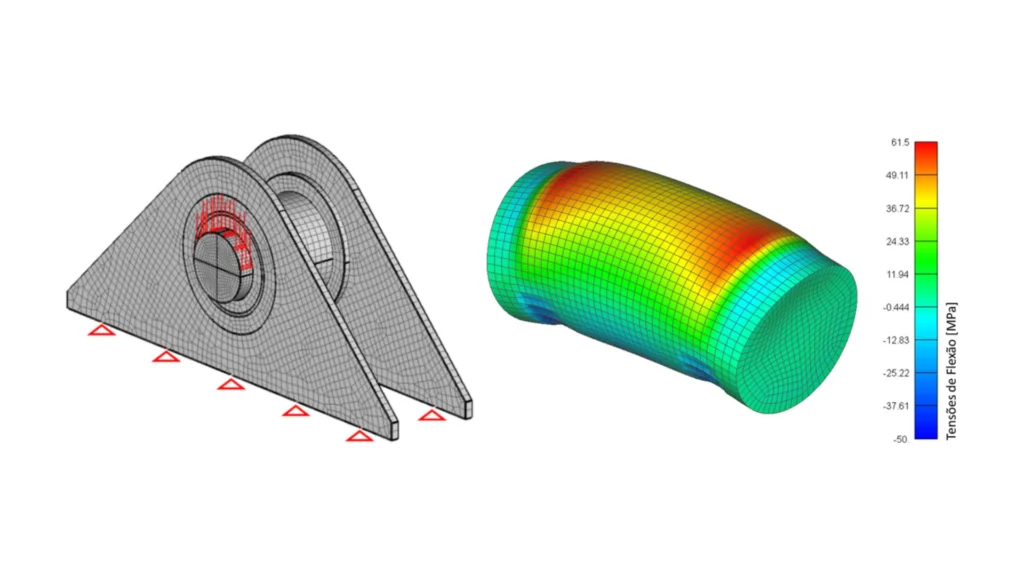
Em razão da inspeção, foi necessário realizar a avaliação da taxa de crescimento da trinca já presente nos pinos, com o intuito de estimar a vida remanescente do componente. Para tanto, a Kot realizou a modelagem dos pinos em elementos finitos para o cálculo das tensões atuantes (vide Figura 11).

Figura 11 – Modelo computacional utilizado nas análises.

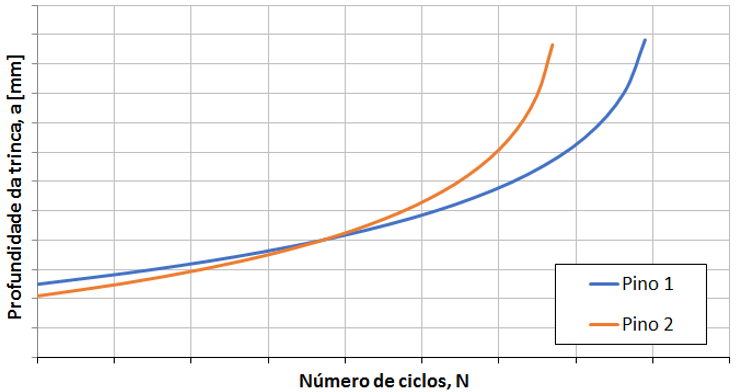
Na análise de mecânica da fratura foi avaliada a variação da profundidade da trinca em função do número de ciclos, conforme ilustrado na Figura 12. Assim, com base nos resultados obtidos na análise, foi possível prever em quanto tempo as trincas atingiriam o tamanho crítico. A partir disso, a Kot sugeriu ações para monitoramento do ativo.

Figura 12 – Variação da profundidade da trinca em função do número de ciclos.

Análise de mecânica da fratura de moinhos SAG e de bolas

A Kot Engenharia realizou a verificação estática e de fadiga, considerando a mecânica da fratura, de moinhos SAG e de Bolas, contemplando cilindro, tampas, flanges e munhões.

Para a determinação das tensões máximas atuantes nos diversos componentes do moinho, foram utilizadas as combinações mais críticas obtidas na análise por elementos finitos. Já a vida útil das soldas entre flanges do corpo e das tampas, bem como entre tampas e munhões, foi verificada pela técnica da mecânica da fratura.

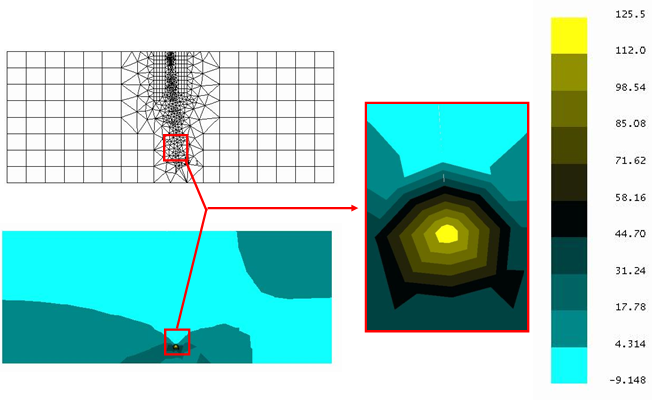
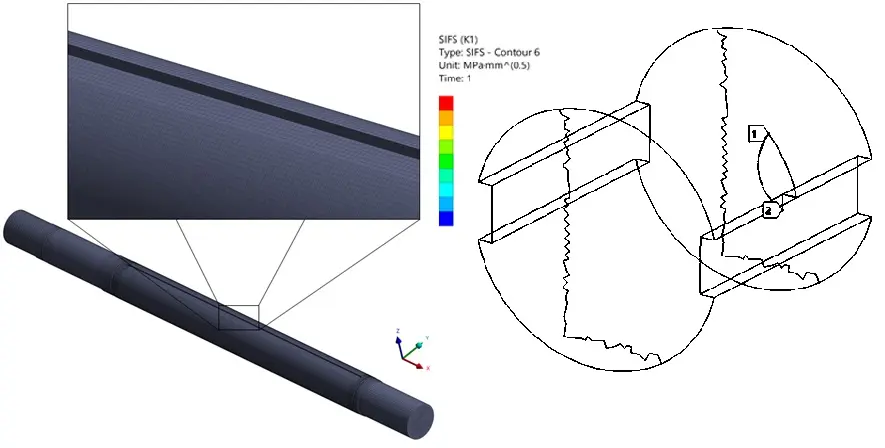
Ambos os moinhos foram analisados considerando a deformada da estrutura após a aplicação dos carregamentos (vide Figura 13), a deformada de várias regiões após a propagação das trincas (vide Figura 14) e o estado de tensões na ponta da trinca (vide Figura 15). Para cada uma das regiões analisadas por mecânica da fratura nos moinhos, foi realizado um cálculo de propagação da trinca para determinação da vida.

A partir dos resultados, foram recomendadas medidas de monitoramento e inspeção para os ativos.

Figura 13 – Deslocamentos do Moinho de Bolas [mm].

Figura 14 – Deformada da região de interesse após propagação da trinca.

Figura 15 – Campo de tensões na região de interesse após a propagação da trinca.

Conclusão

A fadiga estrutural continua sendo um dos principais desafios da engenharia industrial moderna, especialmente em equipamentos submetidos a carregamentos cíclicos e longos períodos de operação. A experiência prática demonstra que análises tradicionais nem sempre são suficientes para capturar os mecanismos de falha presentes em estruturas reais.

Nesse sentido, a Mecânica da Fratura Linear Elástica se destaca como uma ferramenta robusta e confiável para a avaliação da integridade estrutural, estimativa de vida útil remanescente e embasamento de decisões técnicas relacionadas à inspeção, manutenção e operação segura de equipamentos industriais. A existência de trincas em uma estrutura nem sempre demanda intervenção imediata ou mesmo paralisação do equipamento.

A Kot Engenharia atua de forma especializada na aplicação de metodologias de cálculo avançadas, combinando conhecimento normativo, análise computacional e experiência prática para apoiar seus clientes na prevenção de falhas, no aumento da confiabilidade operacional e na otimização dos custos de manutenção.

Para saber como essas soluções podem ser aplicadas aos seus ativos, entre em contato com a nossa equipe.

Siga, também, nossas páginas no LinkedIn, Facebook e Instagram e continue acompanhando nossos conteúdos.